Distribute layers in shape of sphere
Posted: February 10th, 2005, 10:38 am
This expression spreads layers in a 3D space to form a sphere. How does it do it? Simply by cutting a sphere in circular slices. These slices are, in my expression, the "rows". The "middle" slice is row 0, the slice above is row 1, and so forth.
As you can notice, apart from row 0, all the other rows are made of two slices.
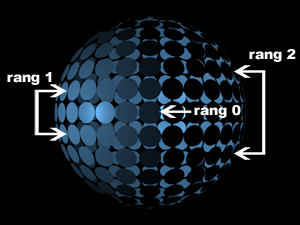
The sphere is symetrical to the place (x/z) containing row 0. My expression uses this symetry to facilitate the construction of the sphere.
Let's take a closer look :
The Null object "A" is in the middle of the sphere and is the parent of all the other layers. This allows to easily move and orient the sphere.
The value "a" allows to manage the space between two layers.
For the sphere to be perfectly homogeneous, this space has to be identical for all layers.
That is the first problem we encounter, because the radius of a slice depends on its row. Thus the spacing angle too.
The image below illustrates this problem : we want the AB distance to be equal to the A'B' distance.
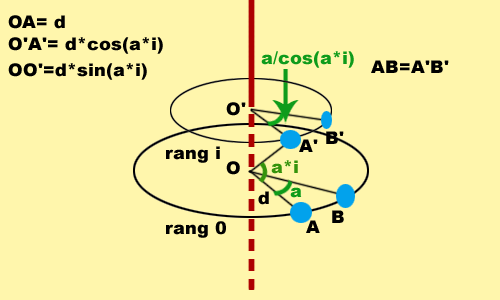
The radius of the "middle" slice (row 0) is d, the radius of the sphere.
But the radius of the i slice (row i) is d*cos(a*i).
So we obtain the following equation :
Where x is the spacing angle to row i.
So we get :
The second difficulty is the amount of layers per slice. The answer is simple, it is
For it to always be an integer, I added the Math.round function :
From there one has to adjust the spacing angle for each row, which becomes :
The symetry is obtained with the function Math.pow, Math.floor is the number of the layer : index-2 or n (n is the number of the layer, the first layer of the sphere is number 1...etc).
Here are the two lnes of code that create this symetry :
and
I hope this helped
Thanks
You can download the project:
http://oscarvideo.free.fr/sphereoscarus.zip
As you can notice, apart from row 0, all the other rows are made of two slices.

The sphere is symetrical to the place (x/z) containing row 0. My expression uses this symetry to facilitate the construction of the sphere.
Let's take a closer look :
The Null object "A" is in the middle of the sphere and is the parent of all the other layers. This allows to easily move and orient the sphere.
The value "a" allows to manage the space between two layers.
For the sphere to be perfectly homogeneous, this space has to be identical for all layers.
That is the first problem we encounter, because the radius of a slice depends on its row. Thus the spacing angle too.
The image below illustrates this problem : we want the AB distance to be equal to the A'B' distance.

The radius of the "middle" slice (row 0) is d, the radius of the sphere.
But the radius of the i slice (row i) is d*cos(a*i).
So we obtain the following equation :
Code: Select all
d*a=d*cos(a*i)*x
So we get :
Code: Select all
x=a/cos(a*i)
Code: Select all
2*Math.PI/spacing angle
Code: Select all
s=Math.round(2*Math.PI/(a/Math.cos(a*i)))
Code: Select all
u=2*Math.PI/s
Here are the two lnes of code that create this symetry :
Code: Select all
symétrie : y=u*Math.floor((index-2)/2)
Code: Select all
d*Math.sin(a*rang)*Math.pow(-1,index-2)
Thanks
You can download the project:
http://oscarvideo.free.fr/sphereoscarus.zip